hy30nq's blog
[혼공머신 / 2주차] 머신러닝 회귀 알고리즘 완벽 가이드: K-최근접 이웃부터 선형 회귀, 릿지와 라쏘까지 본문
아래 글에서는 지도 학습 알고리즘 중 ‘회귀(regression)’ 영역을 중심으로, K-최근접 이웃 회귀부터 선형 회귀, 다항 회귀, 그리고 규제(릿지와 라쏘)까지 폭넓게 다루어보겠습니다. 머신러닝 이론과 함께 scikit-learn(사이킷런), Numpy(넘파이), pandas(판다스) 등의 라이브러리를 활용할 때 알아두면 좋은 내용들을 자세히 정리했으니, 끝까지 읽으셔서 머신러닝 회귀 모델에 대한 전반적인 감을 잡아가시길 바랍니다.
1. 지도 학습 알고리즘이란?
머신러닝 알고리즘은 크게 지도 학습(Supervised Learning), 비지도 학습(Unsupervised Learning), 그리고 강화 학습(Reinforcement Learning)으로 나눌 수 있습니다. 그중 지도 학습은 입력(특성, Feature)과 출력(레이블, Label) 데이터가 주어져 있을 때, 이 둘의 관계를 학습하여 보지 못한 새로운 입력에 대한 출력을 예측하는 학습 방식입니다.
1.1 분류(Classification)와 회귀(Regression)
- 분류(Classification)
출력(타깃)이 정해진 클래스(범주) 중 하나로 분류되는 문제입니다. 예를 들어 개와 고양이를 구별하는 이미지 분류, 이메일이 스팸인지 아닌지 판별하는 문제 등이 대표적인 예시입니다. - 회귀(Regression)
출력(타깃)이 연속적인 수치를 예측하는 문제입니다. 예를 들어 내일의 기온이나 주식 가격, 어떤 제품의 판매량 같은 값들을 예측하는 것이 회귀의 대표적인 사례입니다.
- 타깃값 자체가 연속 수치라는 점에서 분류 문제와 다릅니다.
2. K-최근접 이웃 회귀(K-Nearest Neighbors Regression)
지도 학습에서 간단하면서도 직관적인 알고리즘 중 하나가 바로 k-최근접 이웃(KNN, k-Nearest Neighbors)입니다. 분류에서 많이 알려진 알고리즘이지만, 회귀 문제에도 동일한 원리를 적용할 수 있습니다. 이를 K-최근접 이웃 회귀라고 부릅니다.
2.1 알고리즘 개념
- 예측하고자 하는 새로운 데이터 포인트가 주어지면,
- 학습 데이터(훈련 세트) 중 이 새로운 데이터 포인트와 가장 가까운 k개의 이웃을 찾습니다.
- 찾은 이웃들의 타깃값(정답으로 알려진 출력값)을 평균하여 최종 예측값으로 삼습니다.
예를 들어, k=3이라면 가장 가까운 3개의 샘플을 찾고 이 세 샘플의 타깃값 평균이 예측값이 됩니다.
2.2 scikit-learn에서의 사용법
from sklearn.neighbors import KNeighborsRegressor
knr = KNeighborsRegressor(n_neighbors=3) # k=3으로 설정
knr.fit(X_train, y_train) # 모델 훈련
predictions = knr.predict(X_test) # 예측n_neighbors: 이웃의 개수를 지정하는 하이퍼파라미터(Hyperparameter)- 이외에
weights,algorithm,metric등도KNeighborsClassifier와 유사합니다.
2.3 과대적합과 과소적합
- 과대적합(Overfitting): 훈련 세트에 너무 특화(집착)된 나머지, 새로운 데이터(테스트 세트)에서는 성능이 낮아지는 현상입니다.
- KNN에서n_neighbors가 너무 작을 경우(예: 1), 훈련 세트에 너무 정확히 맞추어버리는 과대적합이 발생할 수 있습니다. - 과소적합(Underfitting): 훈련과 테스트 세트 모두에서 성능이 낮은 경우입니다.
- KNN에서n_neighbors가 지나치게 큰 경우(예: 100), 다수의 이웃 평균에 의해 예측값이 지나치게 단순해져, 좋은 성능을 내지 못할 수 있습니다.
3. 회귀 분석의 성능 지표
3.1 결정 계수(R², Coefficient of Determination)
회귀 모델의 성능을 대표적으로 나타내는 지표가 결정 계수(R²)입니다.
R² 점수가 1에 가까울수록 예측이 정확하다고 볼 수 있으며, 0 또는 그 이하라면 매우 부정확한 모델을 의미합니다.
[
R^2 = 1 - \frac{\sum(\text{타깃} - \text{예측값})^2}{\sum(\text{타깃} - \text{타깃 평균})^2}
]
- 1에 가까울수록 좋다.
- 0에 가까울수록(혹은 음수가 될 수도 있음) 모델 성능이 나쁘다고 해석할 수 있다.
scikit-learn에서 score() 메서드를 사용하면 기본적으로 R² 점수를 계산해줍니다.
3.2 추가적인 회귀 평가 지표
- MAE(Mean Absolute Error): 평균 절댓값 오차
[
\frac{1}{N}\sum_{i=1}^{N} |y_i - \hat{y}_i|
]
절댓값을 취해 오차를 계산하기 때문에, 예측값에서 얼마나 벗어났는지 직관적으로 이해하기 쉽습니다. from sklearn.metrics import mean_absolute_error mae = mean_absolute_error(y_test, predictions)- MSE(Mean Squared Error): 평균 제곱 오차
[
\frac{1}{N}\sum_{i=1}^{N} (y_i - \hat{y}_i)^2
]
제곱을 취해 오차가 클수록 더욱 큰 패널티를 주는 지표입니다. from sklearn.metrics import mean_squared_error mse = mean_squared_error(y_test, predictions)
4. Numpy(넘파이)와 배열 변환
머신러닝에서 사용되는 훈련 세트(X_train, y_train)와 테스트 세트(X_test, y_test)는 2차원 배열 형태여야 합니다. 만약 1차원 배열을 2차원으로 바꾸고 싶다면 reshape() 메서드를 사용합니다.
import numpy as np
test_array = np.array([1, 2, 3, 4])
reshaped_array = test_array.reshape(2, 2)
print(reshaped_array)np.reshape(test_array, (2, 2))와test_array.reshape(2, 2)는 동일합니다.- reshape 전후 원소 개수가 동일해야 합니다. 즉, 원소 수가 맞지 않으면 에러가 발생합니다.
5. 선형 회귀(Linear Regression)
회귀 모델 중 가장 기본이 되는 모델이 바로 선형 회귀입니다. 선형 방정식을 통해 특성과 타깃 간의 최적의 관계(가중치, 계수, 절편 등)를 찾는 방식을 사용합니다.
5.1 1차원 선형 회귀
특성이 하나만 있을 때(1차원)에는 단순 선형 방정식이 됩니다:
[
y = a \times x + b
]
a를 기울기(계수, coefficient)b를 절편(intercept)
이라 부릅니다.
5.2 사이킷런(Scikit-learn)에서의 사용
from sklearn.linear_model import LinearRegression
lr = LinearRegression()
lr.fit(X_train, y_train)
print("계수(coef_):", lr.coef_)
print("절편(intercept_):", lr.intercept_)coef_: 특성별 계수 값(배열 형태)intercept_: 절편(단일 실수 값)
모델 파라미터(model parameter)
- 선형 회귀가 찾는 계수(coef_)와 절편(intercept_)처럼, 머신러닝 모델이 훈련을 통해 ‘학습’하는 파라미터를 의미합니다.
6. 다항 회귀(Polynomial Regression)
선형 회귀 모델이라 해서 반드시 직선(1차방정식)만 활용하는 것은 아닙니다. 다항식(Polynomial)을 사용해 보다 복잡한 패턴도 선형 회귀로 표현할 수 있는데, 이를 다항 회귀라고 합니다.
6.1 다항식 표현
[
y = w_0 + w_1 x + w_2 x^2 + w_3 x^3 + \cdots + w_d x^d
]
이 식은 비선형 함수로 보이지만, 실제로는 x, x^2, x^3 등을 새로운 특성으로 간주하는 선형 모델이므로 여전히 선형 회귀의 형태로 볼 수 있습니다.
6.2 특성 공학(Feature Engineering)
다항 회귀는 기존 특성을 조합해 새로운 특성을 만드는 전처리 과정을 수반합니다. 예를 들어, 기존에 x 하나만 있었다면 x², x³, ... 등을 추가 특성으로 만듦으로써 모델이 더 복잡한 곡선을 학습할 수 있도록 돕습니다.
from sklearn.preprocessing import PolynomialFeatures
poly = PolynomialFeatures(degree=2, include_bias=True)
X_poly = poly.fit_transform(X)
# X가 [[x1], [x2], [x3], ...] 식으로 들어있다면
# X_poly에는 [[1, x1, x1^2], [1, x2, x2^2], [1, x3, x3^2], ...] 형태로 변환degree: 만들 최고차수 지정 (기본값=2)include_bias: 상수항(1) 포함 여부 (기본값=True)
7. 규제(Regularization)
머신러닝 모델을 훈련할 때, 모델이 훈련 세트를 과도하게 학습(과대적합)하지 않도록 하는 장치를 규제(Regularization)라고 합니다.
7.1 릿지(Ridge)와 라쏘(Lasso)
- 릿지(Ridge): 계수(가중치)를 제곱하여 규제를 가합니다.
- 라쏘(Lasso): 계수의 절댓값을 기준으로 규제를 가합니다.
공통점
- 계수의 크기를 줄여 모델이 너무 훈련 데이터에만 맞춰지는 것을 방지합니다.
- 하이퍼파라미터인
alpha값으로 규제의 강도를 조절할 수 있습니다.
차이점
- 릿지는 계수를 0에 가깝게 만들지만, 실제로 0이 되기보다는 아주 작은 값을 유지합니다.
- 라쏘는 계수를 0으로 완전히 만들어 일부 특성을 제거하기도 합니다(희소성, Sparse).
7.2 적절한 alpha 값 찾기
- alpha가 클수록 규제 강도가 세져서 과대적합이 줄어들지만, 너무 크면 과소적합이 발생할 수 있습니다.
- alpha가 작을수록 규제가 약해지므로 과대적합 위험은 있지만, 더 복잡한 모델을 학습할 수도 있습니다.
따라서, 훈련 세트와 테스트 세트의 성능을 비교하면서 가장 균형 잡힌 지점을 찾는 것이 중요합니다.
8. 사이킷런에서 릿지(Ridge) & 라쏘(Lasso) 회귀
8.1 릿지 회귀(Ridge)
from sklearn.linear_model import Ridge
ridge = Ridge(alpha=1.0)
ridge.fit(X_train, y_train)
print("Ridge coef_:", ridge.coef_)
print("Ridge intercept_:", ridge.intercept_)alpha: 규제 강도solver: 최적화 방법 (기본값은auto)
8.2 라쏘 회귀(Lasso)
from sklearn.linear_model import Lasso
lasso = Lasso(alpha=1.0, max_iter=1000)
lasso.fit(X_train, y_train)
print("Lasso coef_:", lasso.coef_)
print("Lasso intercept_:", lasso.intercept_)alpha: 규제 강도max_iter: 알고리즘의 반복 횟수 (기본값=1000)- 라쏘는 좌표 하강법(Coordinate Descent)을 사용하여 최적화를 진행합니다.
9. pandas(판다스)로 데이터 다루기
9.1 CSV 파일 읽기
import pandas as pd
df = pd.read_csv('data.csv',
sep=',', # 구분자
header=0, # 열 이름으로 사용할 행 번호 (0이면 첫 번째 행)
skiprows=0, # 건너뛸 행의 개수
nrows=None) # 읽을 행의 개수 (None이면 전체 읽기)sep,header,skiprows,nrows등의 매개변수를 적절히 사용하면, 다양한 형태의 CSV 파일을 쉽게 처리할 수 있습니다.
9.2 DataFrame과 머신러닝
- pandas의 DataFrame 구조를 이용하면, 분석에 필요한 다양한 전처리를 편리하게 수행할 수 있습니다.
- 최종적으로 모델에 입력하기 위해선 Numpy 배열 형태로 변환(
.values속성 사용 등)하거나, scikit-learn의 여러 변환기를 거쳐 사용합니다.
10. 정리: 머신러닝 회귀 모델의 핵심 포인트
- 데이터 전처리
- 결측값 처리, 이상값 처리, 스케일링(정규화) 등
- pandas, numpy를 사용해 훈련 세트와 테스트 세트를 잘 준비하는 것이 중요
- 모델 선택
- K-최근접 이웃 회귀: 단순하고 이해하기 쉬우나, 거리 계산에 의존적
- 선형 회귀: 해석이 쉽고, 다항 특성과 규제 등을 적용할 수 있어 유연
- 릿지, 라쏘: 규제를 통해 과대적합을 방지하고, 일반화 성능을 높임
- 성능 평가
- R², MAE, MSE, RMSE 등 다양한 지표 활용
- 훈련 세트와 테스트 세트 성능이 비슷한지 비교해 과대적합·과소적합 여부를 판단
- 하이퍼파라미터 튜닝
- KNN의
n_neighbors - 릿지·라쏘의
alpha - PolynomialFeatures의
degree등 - 최적의 값 탐색은 교차 검증(Cross-validation)이나 시각화를 통해 진행
- KNN의
- 주기적인 재훈련
- 데이터가 계속 바뀌는 환경(예: 웹서비스, 유저 데이터)에서는 주기적으로 모델을 업데이트해야 최신 패턴을 잘 반영할 수 있음
11. 예시 코드: 간단한 회귀 분석 워크플로우
아래는 간단한 예시 코드로, 다항 회귀 + 릿지 모델을 이용해 훈련하고 평가까지 수행하는 과정을 담았습니다.
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import Ridge
from sklearn.metrics import r2_score, mean_squared_error
# 1. 데이터 불러오기 (예시로 가상의 csv 파일 사용)
df = pd.read_csv('data.csv')
X = df[['feature']] # 예시로 'feature' 컬럼만 사용
y = df['target']
# 2. 훈련 세트, 테스트 세트 분리
X_train, X_test, y_train, y_test = train_test_split(X, y,
test_size=0.2,
random_state=42)
# 3. 다항 특성 생성
poly = PolynomialFeatures(degree=3, include_bias=True) # 3차 다항식
X_train_poly = poly.fit_transform(X_train)
X_test_poly = poly.transform(X_test)
# 4. 릿지 회귀 모델 훈련
ridge = Ridge(alpha=1.0, solver='auto')
ridge.fit(X_train_poly, y_train)
# 5. 예측
y_pred = ridge.predict(X_test_poly)
# 6. 성능 평가
r2 = r2_score(y_test, y_pred)
mse = mean_squared_error(y_test, y_pred)
print("R^2 Score:", r2)
print("MSE:", mse)
print("Coef:", ridge.coef_)
print("Intercept:", ridge.intercept_)12. 마무리 및 과제
머신러닝에서 회귀(Regression) 문제는 범용적으로 많이 사용되는 중요한 영역입니다. K-최근접 이웃 회귀, 선형 회귀, 다항 회귀, 그리고 릿지(Ridge), 라쏘(Lasso) 등 규제 기법을 적절히 활용하면 다양한 상황에서 예측 성능을 높일 수 있습니다.
- Numpy reshape: 훈련 세트가 2차원 형태여야 할 때 필수적으로 사용
- scikit-learn KNeighborsRegressor, LinearRegression, Ridge, Lasso 등: 각 상황에 맞는 다양한 모델들
- 결정 계수(R²): 회귀 모델의 대표적인 성능 지표
- Mean Absolute Error(MAE), Mean Squared Error(MSE): 예측 오류를 측정하는 지표
- 과대적합(Overfitting) vs 과소적합(Underfitting): 하이퍼파라미터 설정을 통해 적절히 제어
- 규제(Regularization): 릿지와 라쏘를 활용해 모델 일반화 성능 개선
- pandas read_csv: 다양한 매개변수로 CSV 파일을 유연하게 읽고 전처리
이 글에서는 지도 학습에서의 회귀 알고리즘과 머신러닝 모델 훈련 과정에 대해 폭넓게 살펴보았습니다. 실제 프로젝트에 적용할 때에는 도메인 지식, 특성 공학, 적절한 모델 선택이 특히 중요합니다. 이를 위해 꾸준히 데이터를 탐색하고, 모델을 검증하면서 지속적으로 개선해나가면 훌륭한 예측 모델을 구축할 수 있을 것입니다.
과제
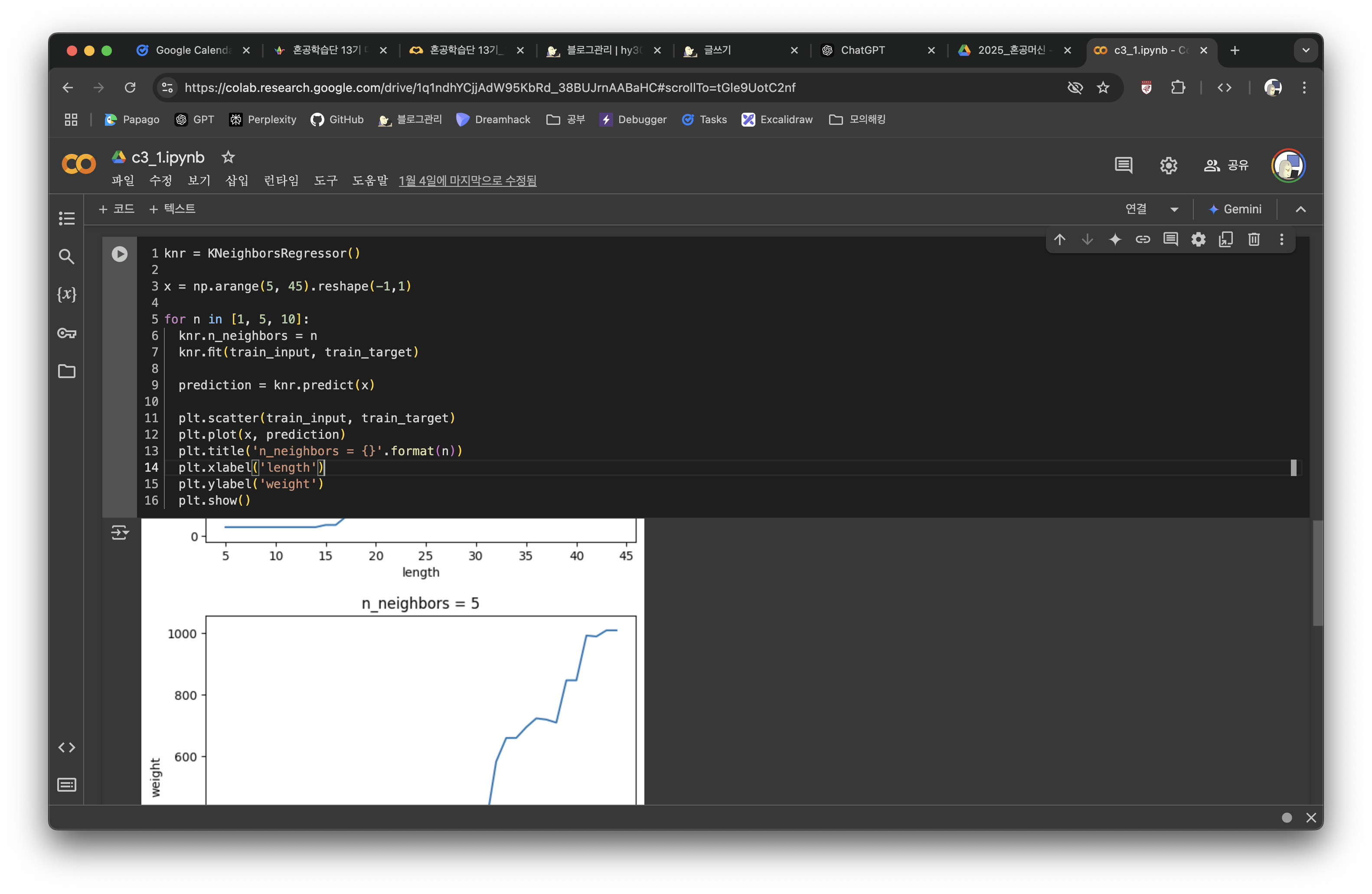
추가 자료 & 참고 링크
'대외 활동 > 혼공학습단' 카테고리의 다른 글
| [혼공머신 / 1주차] 인공지능부터 k-최근접 이웃(KNN)까지, 머신러닝 핵심 개념 총정리 (2) | 2025.01.09 |
|---|---|
| [혼공네트] 5주차_정리 (0) | 2024.08.10 |
| [혼공네트] 4주차_정리 (0) | 2024.07.25 |
| [혼공네트] 3주차_정리 (0) | 2024.07.19 |
| IPv4의 대표적인 기능과 라우팅 프로토콜에 대해서 (0) | 2024.07.16 |




